По правилам проект-конкурса, набравший наибольшее количество баллов по итогам месяца участник награждается специальным призом. Наибольшее количество баллов за июль набрала Салимат Чалабова. Справедливости ради следует сказать, что Салимат включилась в участие проекта только в последние два месяца, но тем не менее уверенно вышла в лидеры. За месяц она набрала рекордное количество – 1180 баллов. Во вторник, 5 августа в 14:00, мы ждём победителя в торговом зале магазина цифровой техники «Москва Сити» в Махачкале по ул. Чернышевского, 115, для вручения приза. Подробнее об условиях награждения можно узнать по тел.: 8-988-291-08-50.
Первый приславший правильный ответ зарабатывает дополнительно к баллам за задание ещё 10 %. Ответы, отправленные не позже четверга следующей недели, но не дошедшие до редакции вовремя, также будут учтены и занесены в базу данных. Каждый участник, набравший наибольшее количество баллов по итогам месяца, тоже награждается призом от спонсора проекта – магазина «Москва Сити». У вас есть возможность увидеть свои накопленные баллы в рейтинговой шкале на нашем сайте www.chernovik.net. База данных обновляется каждую пятницу.
Ответы вы можете присылать на e-mail: sl007@mail.ru
Результаты участников проект-конкурса за прошлый номер
1. Магомед Гаджиев – 268 баллов
2. Lord Bizard – 264 баллов
3. Гаджигерей Гаджигереев – 262,5 баллов
4. Салимат Чалабова – 256 баллов
5. Ислам Абдуллаев – 256 баллов
6. Этери Iteri – 256 баллов
7. Адриано Ибрагимов – 256 баллов
8. Бастамин Магомедов – 256 баллов
9. Гусейн Сулейманов – 256 баллов
10. Тагират Магомедова – 256 баллов
11. Фарида Абакарова – 256 баллов
12. Эльнара Абдуллаева – 256 баллов
13. amikys – 256 баллов
14. Аслан Биячуев – 256 баллов
15. Мизана Алиева – 256 баллов
16. Муслим Закарьяев – 256 баллов
17. Хайбула Гитихмадибиров – 256 баллов
18. Шапи Рабаданов – 256 баллов
19. Мутаалим Хайбулаев – 256 баллов
20. Велибек Мамедов – 256 баллов
21. Ахмед Амирбеков – 256 баллов
22. Мурад Юхаранов – 256 баллов
23. Магомед Ханжаров – 256 баллов
24. Асад Басаев – 256 баллов
25. Магомед Махмудов – 256 баллов
26. Асият Султанова – 256 баллов
27. Яраги Омаров – 256 баллов
28. «избербашец» – 256 баллов
29. Амиран Марданов – 256 баллов
30. Persona non grata – 256 баллов
31. Iljas copala – 256 баллов
32. Рашид Абдурахманов – 256 баллов
33. «Фуксия» – 256 баллов
34. «Евгений» – 256 баллов
35. Мурад Алейдаров – 256 баллов
36. Zubair 72 – 200 баллов
37. Таня Чермошенцева – 200 баллов
38. Зухра Абдулатипова – 200 баллов
39. Руслан Османов – 200 баллов
40. Абдула Исаев – 200 баллов
41. Ислам Исаев – 185 баллов
42. Расул Омаров – 185 баллов
43. badpauk@mail.ru – 185 баллов
44. М-гаджи – 185 баллов
45. Абдулкарим Исмаилов – 185 баллов
46. Саида Мурсалова – 185 баллов
47. Чупан Эльдаров – 185 баллов
48. Джамиля Муртузалиева – 125 баллов
49. Тимур Пирбудагов – 125 баллов
50. Магомед Гусейнов – 125 баллов
51. Неби Велиев – 120 баллов
52. Смит – 120 баллов
53. Эльдар Мурадов – 120 баллов
54. erty – 120 баллов
55. Мурад Ибрагимов – 120 баллов
56. Диана Магомедова – 120 баллов
57. «Рома Букин» – 120 баллов
Как связать верёвки
С потолка, не касаясь пола, свисают две верёвки. Расстояние между их концами достаточно велико. Во всяком случае, держась за один конец верёвки, нельзя дотянуться до конца другой верёвки. Тем не менее верёвки можно соединить друг с другом на высоте, не превосходящей человеческого роста. Задача состоит в том, чтобы связать концы верёвок, не пользуясь ничем, кроме ножниц.
Полюсом холода на территории России считается якутское селение Оймякон, где зафиксированы температуры ниже 70 градусов мороза. А есть ли на Земле место, где ртутный столбик термометра показывает ещё более низкую температуру, чем в России? Если есть, то где именно (только указать континент недостаточно).
[военная головоломка] 65 баллов
В начале Первой мировой войны в униформу британских солдат входила коричневая матерчатая фуражка. Металлических касок у них не было. Через некоторое время командование армии было обеспокоено большим количеством ранений в голову. Было решено заменить фуражку металлической каской. Но вскоре командование было удивлено, узнав, что количество ранений в голову увеличилось. Необходимо заметить, что интенсивность сражений была примерно одинаковой до и после введения касок. Так почему же число ранений в голову увеличилось, когда солдаты стали надевать каски, а не фуражки?
На рисунке представлен квадрат 13х13, состоящий из 169 маленьких квадратиков. Сожете ли вы разделить этот большой квадрат на меньшие квадраты? При этом линии должны проходить по границам маленьких квадратов. Например, большой квадрат можно разделить на 22 квадрата (3 квадратa 4х4, 12 – 3х3, 2 – 2х2, 5 – 1х1), но можно ли добиться того, чтобы их было менее 20? А как надо разделить большой квадрат, чтобы получить наименьшее количество меньших квадратов, и чему равно их число?
[Ответы на задания предыдущего номера]
Легче или тяжелее?
Взвешиваем 50 и 50 монет:
1) Равенство:
Беpём оставшуюся монету и ставим её в левую кучку вместо одной из имеющихся там.
1.1 Левая кучка тяжелее – фальшивая монета тяжелее.
1.2 Левая кучка легче – фальшивая монета легче.
2) Hеpавенство:
Беpём более тяжёлую кучку и разбиваем её на две кучки по 25 монет.
2.1 Вес кучек одинаковый – фальшивая монета легче.
2.2 Вес кучек неодинаковый – фальшивая монета тяжелее.

Нам нужно найти сумму всех нечётных чисел от 1 до 2n-1 и убедиться, что она равна n
2. Это можно сделать разными способами. Мы предпочли геометрический. Возьмём квадрат из n
2 клеток и закрасим клетки так, как это сделано на рисунке для n = 6. Квадрат при этом распадается на чередующиеся по цвету участки. Сосчитаем количество клеток в них, начиная с левого верхнего угла. Первый участок состоит из одной клетки, второй – из трёх клеток, третий – из пяти и т. д., последний n-й участок состоит из 2n-1 клеток. Следовательно, число клеток в квадрате равно:
1 + 3 + 5 + 7 + ... + 2n-1
Это убеждает нас, что нужное равенство выполнено всегда.
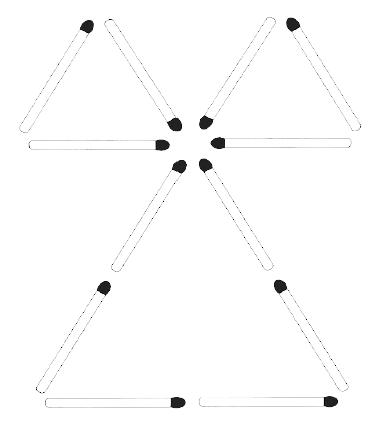
Спички