Отправляйте ваши ответы по адресу:
367000, Махачкала, ул. М. Гаджиева, 94,
2-й эт., газета «Черновик»
или на e-mail: eruditor@mail.ru.
Последовательность - 60 баллов
Продолжить последовательность чисел
7, 14, 17, 20......
Игра со стержнями - 90 баллов
Имеется 100 деревянных стержней с длинами 1, 2, ..., 100 см. Каждый игрок по очереди выбирает 3 стержня, складывает из них треугольник и сжигает его. Проигрывает тот, кто не может сделать ход. У кого из игроков есть выигрышная стратегия?
Неизвестный газ - 80 баллов
Некий сосуд наполнен очищенным газом, неизвестно каким.
Чтобы поднять температуру 1 кг этого газа на 10С при изобарном процессе требуется подвести 958,4 Дж, а при изохорном – 704,6 Дж.
Какой газ находится в сосуде?
Облава в тоннеле - 100 баллов
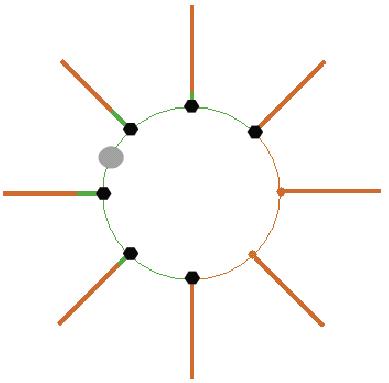
Есть система тоннелей следующей структуры: кольцевой тоннель в форме окружности длиной L + отходящие на одинаковых расстояниях (равномерно по окружности кольцевого тоннеля) n проходов (n – целое неотрицательное число; n=0,1,2…) длиной q (никакой «отходящий» проход ни с чем, кроме кольцевого тоннеля, не пересекается, все «отходящие» проходы одной длины). В этой системе тоннелей находятся двое. Скорость передвижения первого ограничена и очень мала (в тоннелях довольно темно, и он там никогда раньше не был), а скорость передвижения второго может быть сколь угодно велика (он знает их как свои пять пальцев). Они оба знают структуру тоннелей вместе с длинами проходов. Задача первого – обнаружить второго, на котором есть «маячок». Дальность действия маячка – E (при этом он действует только по воздуху, обнаруживаться сквозь стены он не может; кривизна проходов для маячка не важна). Задача второго – не быть обнаруженным. Постарайтесь найти как можно меньшее число E, при котором первый игрок сможет гарантированно (то есть даже в том случае, если второй игрок заранее знает траекторию поиска первого) поймать второго.
Серая точка (побольше) – расположение первого. Звёздочки - располагаясь в которых, второй был бы замечен при таком расположении первого.
Ответы на задания предыдущего номера
1. Коэффициент
невыговариваемости
В первую очередь надо просто посмотреть на структуру числительных. Для многоразрядных чисел это «столько-то миллионов столько-то тысяч столько-то...», причём каждое такое «сколько-то» – это трёхзначное число. В некоторых случаях может быть «миллион», «миллиона» или «миллионов», «тысяч» или «тысячи» в зависимости от того, на какую цифру заканчивается соответствующее число.
Так что задача сводится к поиску наименее выговариваемого трёхзначного числа. Поскольку каждый разряд в русском языке более-менее независим, то можно просто посмотреть на названия ЦИФР. Самыми длинными из ряда
1, 2, 3, 4, 5, 6, 7, 8, 9 получаются четыре, восемь, девять – по 6 букв. Однако во втором разряде (десятки) четвёрка не «канает», потому что «сорок» вдвое короче, чем «девяносто» и «восемьдесят». Заметим попутно, что «девяносто» на две буквы короче, чем «восемьдесят», так что число десятков должно быть 8.
Алгоритм поиска числа с максимальным КН.
Можно искать число, начиная с 1 цифры и дописывая слева. КН = среднему числу букв в названии цифр (на соответствующих местах, естественно), следовательно, добавление новой цифры (или группы цифр) оправдано, только если в ней больше букв, чем текущий КН числа.
Запись 1(234)5 будет означать «любое число из 125, 135, 145».
1-значные: (489) КН= 6/1 =6 (находим перебором)
2-значные: 8(489) КН= 17/2 = 8,5 (приходится перебрать все 11, 12...19, 20, 30,40...90, чтобы найти лучшее значение 84, 88, 89; 8 добавляет 11 букв)
3-значные:(489)8(489) КН=8,67 (перебор; первая цифра добавляет 9 букв)
4-значные:4(489)8(489) КН=9,5 (четыре тысячи – 12 букв, восемь тысяч – только 11)
5-значные 84(489)8(489) КН=9,8 (восемьдесят, как всегда, добавило 11 букв)
6-значные: не имеет смысла, т. к. добавить выходит всего 9 букв при среднем 9,8; лучшие результаты у (489)84(489)8(489) КН=9,67
7-значные: (89)(489)84(489)8(489) КН=10,43 (прорыв за счёт слова «миллионов» на 9 букв; «восемь (или девять) миллионов» дают уже 15 букв, а «четыре миллиона» – только 14)
8-значные 8(89)(489)84(489)8(489) КН=10,5 (снова восемьдесят!)
9-значные – удаётся добавить только 9 букв, что очевидно меньше текущего КН.
Итак, числа-рекордсмены по КН = 10,5 будут иметь вид: 8(89)(489)84(489)8(489)
Всего таких чисел 2*3**3*3 = 54 числа
Примеры:
8(89)(489)84(489)8(489), вместо каждых скобок подставляем одну цифру из них, например: 88484888 – восемьдесят восемь миллионов четыреста восемьдесят четыре тысячи восемьсот восемьдесят восемь – 84 буквы, 8 цифр, КН= 84/8 = 10,5 89884989 – восемьдесят –11 девять –6 миллионов –9 восемьсот –9 восемьдесят –11 четыре –6 тысячи –6 девятьсот –9 восемьдесят –11 девять –6 84 буквы, 8 цифр, КН= 84/8 = 10,5.
И таких чисел с КН = 10,5 будет 54
2. Сапёр
ПРАКТИЧЕСКИЙ АЛГОРИТМ

Ставим мину в центр поля и отмечаем клетки, на которых других мин точно быть не может (четыре клетки, соприкасающиеся с миной по горизонтали и вертикали, и восемь клеток, которые имеют общие рёбра с этими соприкасающимися). Максимально близко к первой мине ставим четыре другие (больше не получится) и тоже отмечаем клетки, где мин быть не может.
Опять как можно ближе добавляем мин и отмечаем клетки, где они находиться не могут.
Итак, имеем 2 варианта с максимальным количеством мин – 17, соответствующие условиям задачи, что является доказательством того, что расположить таким образом 18 мин НЕЛЬЗЯ.
3. Песочные часы
Обозначим часы на 7 минут – 7М, а на 4 минуты – 4М.
Распишем по минутам.
0 минут. 7М – песка на 7 минут, 4М – песка на 4 минуты.
4 минуты. 7М – песка на 3 минуты, 4М – песка на 0 минут.
Переворачиваем 4М и получаем:
7М – песка на 3 минуты, 4М – песка на 4 минуты.
7 минут. 7М – песка на 0 минут, 4М – песка на 1 минуту.
Переворачиваем 7М и получаем: 7М – песка на 7 минут, 4М – песка на 1 минуту.
8 минут. 7М – песка на 6 минут, 4М – песка на 0 минут.
Переворачиваем 7М и получаем: 7М – песка на 1 минут, 4М – песка на 0 минут.
9 минут. 7М – песка на 0 минут, 4М – песка на 0 минут. Ровно 9 минут отсчитано.
4. Шахматное поле

1. Вот таким образом можно разместить 84 фигуры.
Чёрные клетки – пустые (без фигур) = 37.
Белые клетки – с фигурами = 84.
Пустые клетки:
1,9,11 2,6,10 3,9,11 4,6,8
5,6,7 2,4,5,6,7,8,10 5,6,7
4,6,8 1,3,9 2,6,10 1,3,11
11 х 11 = 121 121 – 37 = 84
84 –это максимальное количество фигур, которое можно разместить при данных условиях. В связи с отсутствием полной симметрии в квадрате, доказать это аналитически весьма трудно.
5. Соответствия.
О-Д-Т-Ч-П-Ш-С-В-Д-Д-О-Д-Т-Ч-П-Ш-С-В-Д-Д-............
1-2- 3- 4- 5- 6- 7- 8-9-10-11-.............................



